Example of Rotation of Rigid Bodies:

 A particle is projected along a parabola

                            y ₂  = 4 x

At a definite instant, when flowing through a point P (4, 4) its speed is 5 m/s and the rate of amplify of its speed is 3 m/s2 along the path. Find velocity & acceleration of the particle in terms of rectangular coordinates.

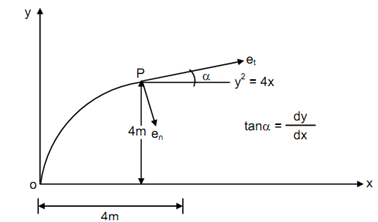
Solution

As the data relate to the path of the particle, the path coordinates can be used to advantage. The unit vectors are related as:

                   e_t  = cos α i + sin α j

                   e_n  = sin α i - cos α j

From the equation of the path y ²dy = 4 x differentiation w. r. t. x results in

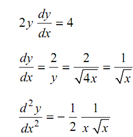
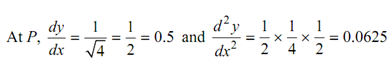
tan α= 0.5  or α= tan ^-1  0.5 = 26.57^o

∴          et = 0.894 i + 0.447  j

and

 en  = 0.447 i - 0.894  j

Velocity of a particle P is given by following

V  = V e_t = 5 (0.894 i + 0.447  j)

               = (4.4 7 i + 2.235 j) m/s

The tangential component of the acceleration is following

a_t  = a_t  e_t

∴ a_t = 3 (0.894 i + 0.447  j)

          = (2.68 i + 1.34  j) m/s²

The normal component of the acceleration is following

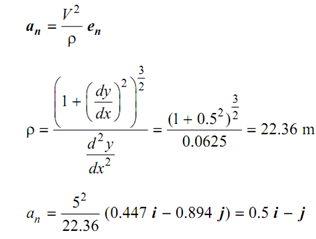
The acceleration is, so, given by

a = a_n  + a_t

= 2.68 i + 1.34 j + 0.5 i - j

= (3.18 i + 0.34 j) m/s²