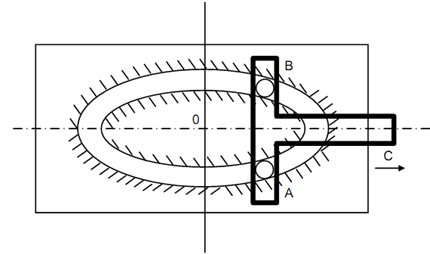
Acceleration of the pins:

Pins A & B ought to always remain in vertical slot of yoke C that moves to the right at a constant speed of 2 m/s as in given figure. These pins remain in an elliptical slot with semi-major & semi-minor axes 3 m & 2 m long respectively. Find out

(a) Speed at which the pins A & B approach each other while yoke slot is 1.5 m from O.

(b) Acceleration of the pins to each other.

Solution

The equation of the elliptical path wherein pins move might be written as

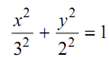
On differentiation

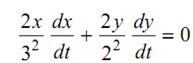
While x = 1.5 m

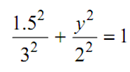
or        

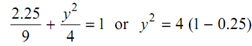
or

y ₂  = 4 (1 - 0.25)

or         y = 2 × 0.866 = 1.732 m

∴        

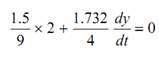
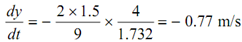
It means that the pin B moves having speeds 0.77 m/s downward. Obviously pin A ought to move upward having speeds 0.77 m/s. Thus, these pins approach each other along a velocity (0.77 + 0.77) or 1.54 m/s.

Differentiating again

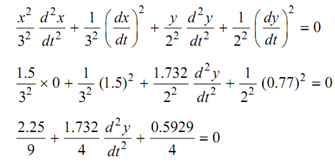
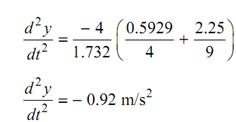
Pin B is accelerating downward at a rate of 0.92 m/s2. At the similar time pin A is accelerating at the similar rate upwards. Thus, pins A and B accelerate to each other by 2 × 0.92 or 1.84 m/s².