Macaulay Duration: Developed in 1938 by Frederick Macaulay, this form of duration measuresthe number of years required to recover the true cost of a bond, considering the present value of all coupon and principal payments received in the future (which is why it is the only type of duration quoted in "years"). It assumes interest rates are continuously compounded. In 1938, Macaulay suggested a method for determining price volatility of bonds. He gave the name duration to the measure, but it is now often called Macaulay duration. The formula that he gave is:

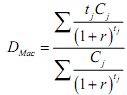
where: D_Mac  is the Macaulay Duration; r is the periodic yield (yield for one period); t_j is the time until the  jth cash flow; C_j is the j_th cash flow; k is the total number of cash flows.
Because of very little volatility of interest rates, as these were regulated, little attention was paid to duration until the 1970s. In the 1980s interest rates started to rise dramatically in the United States. Investors and traders started to look for any tool that would help them to know how much the prices of bonds would change for a given change in yields. Here the concept of duration came in handy.

Macaulay duration can be used to determine the following:

- The duration of a zero coupon bond is equal to its time to maturity.

- The duration of a coupon bearing bond is less than its time to maturity.

- If two bonds have the same coupon rate and yield, then the bond with the greater maturity has the greater duration.

- If two bonds have the same yield and maturity, then the one with the lower coupon rate has the greater duration.