Decision-making under uncertainty:

We just saw what an asset means. We have also discussed asset pricing theories and the features of efficient markets. Markets of several types of assets are characterised by uncertainty. In this section, optimal decision-making in the presence of uncertainty is explained.

We had mentioned earlier that that some economists in the days gone by had made a distinction between situations of risk and that of uncertainty, with the former being situations where the individual could list the outcomes and assign probabilities to these, while uncertainty denoted situations where no such outcomes could be listed and moreover, probabilities could not be assigned. Nowadays such distinctions are not made because, if followed, it would imply that no theoretical analysis would be possible of situations of uncertainty. So what was earlier called situations of risk is now routinely called situations of risk and situation of uncertainty interchangeably. So we basically set out the theory of decision-making under situations of risk; in many expositions these are also called decision-making under situations of uncertainty. What this section does is to take the theory of individual decision-making as set out in microeconomics and extend it to situations of uncertainty. The basic point about decision-making in microeconomic environments is that it assumes that the decision- maker is rational in the sense that the decision-maker wants to optimise (maximise or minimise) certain objective function subject to constraints. For example, the consumer maximises utility subject to the budget constraint while the producer maximises profits or minimises costs. We assume the individual investors, like  the consumer wants to maximise their utility. But while in basic theory of the consumer it is assumed that the consumer's utility function is a function of the goods consumed (more the goods consumed, greater the utility-"more is preferred to less") in situations of uncertainty, utility is a function of something more complex. This is explained below.

While discussing asset pricing theories and mean-variance portfolio analysis, we have discussed decision-making under  uncertainty. While discussing portfolio selection we mentioned that the investor looks at both the mean returns and risk of the  asset, where the variance was taken as a measure of risk. In this section we look at the decision-making by an individual under uncertainty, while keeping utility maximisation as the basic behavioural characteristic. We can think of the different outcomes of some random event as being different states of nature. We just modelled states of nature in the mean- variance portfolio choice. We next think of a contingent consumption plan as being a listing of what the consumer will consume in the different states of  nature each of which is a different outcome of the random process. Consumer/investors have preferences over different plans of contingent consumption, just as they have over actual consumption. Since the consumer has preferences about consumption in  different states, we can use a utility function to describe these preferences. The key here is to frame an appropriate concept of utility function, which will depict correctly the decision-making under uncertainty. We will presently see that the expected utility is the appropriate concept. Presently we will discuss the properties of the expected utility and also certain axioms that expected utility should satisfy. Subsequently, we will develop the concept of attitude towards risk -that is, whether the individual is risk-averse or risk lover or risk-neutral on the basis of the curvature of the expected utility function. Let us now develop the notion of expected utility. For this, let us observe the basic thing that investor/consumer is concerned with probability distribution of getting different consumption bundles of goods. We say utility is a function of wealth, but wealth or consumption has probability distribution, and the consumer has to choose a pattern of probability distribution. People have different preferences over  probability distribution the same way that they have preferences over goods. In situations of uncertainty, we can think of monetary rewards in different situations as different goods. For simplicity, consider two mutually exclusive states s₁  and s₂ and let π₁  and π₂  be probabilities of the occurrences of these states. Since there are only two states, . We can write the utility function as:

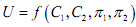
Since the c's are consumption, and the πs are probability, a function such as gives utility as a function of the expected, or average, value of consumption.

If on the other hand we have a utility function like

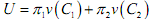
we have the right-hand side expressing the average utility, or expected utility function. This is also known as the von Neumann-Morgenstern utility function after the mathematician von Neumann and economist Oskar Morgenstern, who suggested this form. The expected utility function is a reasonable depiction of utility from consumption under uncertainty because only one of the states  s₁  or s₂  will occur and if s₁  occurs, π₂  will be zero and U =v(C₁ )  and similarly for state 2. A strong assumption is made about the utility function: it is that the choice individuals make in one state of nature is independent of the choices they make in another state of nature. This is called the  independence assumption and it implies that the utility function is additive separable.