Find the maximum and minimum pressure:

A masonry retaining wall of trapezoidal section and earth side face vertical has a top width of 1.5 m and base width of 3.5 m. The wall is 6 m high and retains earth at a slope of 1 vertical to 2 horizontal. The weight of soil retained is 18 kN/m3 and the angle of repose is 30^o.  Find the maximum and minimum pressure intensities at the base of the wall. Weight of masonry is 23 kN/m³.

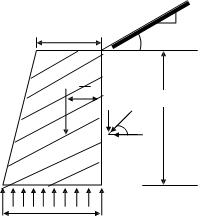
(a) Retaining Wall

(b) Pressure Diagram

Figure

Solution

Considering 1 m width of wall (Figure 12).

tan α = 1/2

∴          α = 26.57^o and cos α = 0.8944

φ = 30^o    ∴ cos φ = 0.866

∴ Coefficient of active earth pressure

= 0.5366

∴          P = Ka            = Wh²/2 = 0.5366 × 18 ×6²/2= 173.87 kN

which is inclined at an angle α = 26.57^o with horizontal.

Horizontal component of P, Ph = P cos α = 173.87 cos 26.57^o = 155.5 kN

Vertical component of P; Pv = P sin α = 173.87 sin 26.57^o =77.7 kN

 and    P acts at a distance h/3 = 6/3 = 2 m above the base.

Weight of masonry wall (per m width),

W = (a + b)/2 ⋅ h ⋅ ρ = (1.5 + 3.5)/2 × 6 × 23 = 345 kN

This acts at a distance of x¯ from C,

 Where x¯ = a² + ab + b²/3(a + b) = 1.317 m

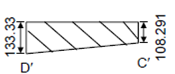
∴          Total pressure acting on point C of that the base will be

Pc= (W/b)+(Pv/b)+ (6W(b/2- x¯)/b²)+(6Pv(b/2)/b² )- (2Ph× h/b²)

= (345/3.5) + (77.7/3.5) +( 6 × 345(1.75 - 1.317)/(3.5)² )+ (6 × 77.7 × 1.75/(3.5)²  )- (2 × 155.5 × 6/(3.5)²)

= 108.21 kN/m²

Or total pressure acting at point D of the base will be

PD= (W/b)+(Pv/b)+ (6W(b/2- x¯)/b²)+(6Pv(b/2)/b² )- (2Ph.h× /b²)