Calculation of Pressures at the Base of Retaining Wall:

In all these calculations we consider 1 m width of the wall. Here P is the total horizontal pressure acting on a retaining wall and W is the total weight of all vertical loads acting on it including its own weight. If the resultant of these forces meet the base at point E and O is the midpoint of the base then OE = e is the eccentricity of the resultant R.

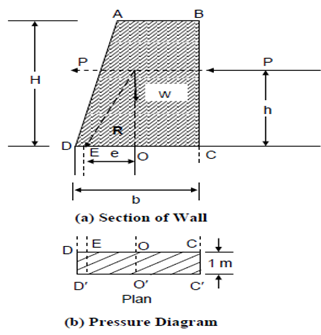
Figure

Therefore, the base will be subjected to an eccentric load caused by a direct vertical load W and a moment M (= Ph ± W.e).

The stress at some point distant x from the centre O will be given by

p = W/A ± M. x/ I₀

where b is the width of base DC, or I₀ that is the moment of inertia of the base rectangle CC′DD′ about the centre line OO′ ( Here I0 =1 × b³/12 = b³/12)

and A (= 1 × b = b) is area of the rectangle CC′DD′.

The extreme pressure (maximum and minimum) acts at the point D and C where, x = b/2 .

Substituting these values in Eq., we have

P_ext      = W/b ±  M(b/2)/b³/12 = W/b ± 6M/b²                                                       

We have p_ext  = W/b ± 6We/b²                                                                                        

Masonry is assumed to be capable of taking compressive stresses but no tensile stresses. As tensile stresses will occur first at the point C (the point of smallest stress) if pc < 0, stress at C is tensile.

or        W/b ± 6W/b² . e < 0 for tensile stress.

or        1 < 6e /b

or        writing it in the other way e > b/6

In other words if the eccentricity is more than b/6 to the left of O there will be tensile stresses at O. (Same, if the eccentricity is more than b/6 to the right of O there will be tensile stresses at D.) Therefore, we see that as long as the resultant lies within the middle third of the base there will not be any tensile stress in the section. This is the famous middle third rule.