Resultant of Coplanar Non-concurrent Forces:

The resultant of a system of coplanar non-concurrent forces can be attained by adding two forces at a time and then combining their sums. The three forces F₁, F₂ and F₃ illustrated in Figure can be combined by first addition up any two forces such as F₂ and F₃. They can be moved along with their lines of action to their point of concurrency A by the principle of transmissibility.

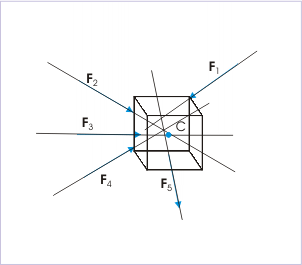
Their sum R₁ is created by the law of parallelogram of forces. The force R₁ can then be combined with F₁ by the parallelogram law at their point of concurrency B to attain the resultant R of the three specified forces. Here, the order of combination of the forces is immaterial as might be demonstrated by combining them in a different sequence. Now, the force R can be applied at any point on its established line of action.

Algebraically, the similar result can be obtained by forming the rectangular components of the forces in any two convenient perpendicular directions. In Figure, the x and y components of R are seen to be the algebraic sums of the respective components of the three forces. Therefore, generally, the rectangular components of the resultant R of a coplanar system of forces can be expressed as

R_x  = ∑ F_x   and       R_y  = ∑ F_y

where,

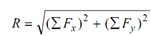
The angle made by R with the x-axis is

θ = tan ^-1 ( ∑ F_y / ∑ F_x)

The position of the line of action of R can be computed with the help of Varignon's theorem. The moment of R (Figure (a)), w.r.t. some point should equal the sum of the moments of its two components F₁ and R₁ around the same point. However, the moment of R₁ should equal the addition of the moments of its components F₂ and F₃ about the similar point. It follows that the moment of R around any point equals the addition of the moments of F₁, F₂ and F₃ around this same point. The application of this principle of moment w.r.t. the point O, illustrated in Figure, gives the equation

                              R d = F₁ d₁ - F₂ d ₂ + F₃ d₃

For this system of forces whereas the clockwise direction has been taken as positive, the distance d is calculated from this relation, and R, whose direction and magnitude have already been find out earlier, might now be completely situated. Generally, then, the moment arm d of the resultant R is specified by

R × d = ∑ M _o        

where ∑ M _o stands for the algebraic addition of the moments of the forces of the system around any point O.

For a system of parallel forces, magnitude of the resultant is the algebraic addition of the various forces, and the location of its line of action can be obtained from the principle of moments.

Now, let a force system such as illustrated in Figure where the polygon of forces closes and as a result there is no resultant force R. Direct combination through the law of parallelogram illustrates that for the case illustrated, the resultant is couple of magnitude F₃d. The value of the couple is equivalent to moment sum w.r.t. any point. Hence, it is seen that the resultant of a non-concurrent coplanar system of forces can be either a force or a couple.