Lagrange Interpolation:
This technique is fairly useful for programming in digital computer. In this, a revised form of quadratic equation (called the 2nd order Lagrange polynomial) is utilized. Here (x1, y1), (x2, y2) and (x3, y3) are the data points available to determine the three constants
i.e., y = f (x) = c1 (x - x2) (x - x3) + c2 (x - x1) (x - x3) + c3 (x - x1) (x - x2)
By setting x = x1, x2 and x3, we have
c1 = y1 / (( x1 - x2 ) ( x1 - x3 ))
c2 = y2/(( x2 - x1 ) ( x2 - x3 ))
c3 = y3 / (( x3 - x1 ) ( x3 - x2) )
The general form of the n - 1 degree Lagrangian polynomial is
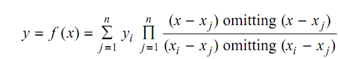
where the sign Π denoted multiplication.