Normal Form Games:

Generally,  in  normal form games players chose their  strategies simultaneously and the combination of strategies chosen by  each player  determine payoff for each player. Thus, normal form game specifies 

1)  A set of players 

2)  Pure strategy space  for  each player  denoted  by  S,  (the subscript  i  denotes the ith  player) 

s_i ∈ S_j (Read si belongs to S_i)

where, si  is an element of S_i, 

3)  Payoff  fhnction  of  the game. This  function  determines what  the  players will get in her hand after the players have chosen their strategies. For firms it could be  profits, for consumers  it could be  utility etc. Payoff of a player is  a  function  of  strategies  simultaneously chosen  by  her and  the  other players. 

 is  the payoff function of the  ith player where,  s= (s₁, s₂, s₃,.  . . .  .  . S_(n-1), s_n)  is the vector of strategies where si  is the strategy picked up by the ith  player.  

In  this kind of game we assume that 1)  each player knows the game 2) each player is rational. Rationality is common  knowledge. That  is  the  ith player knows that her rival knows that she is rational. Definition: The normal form representation  of a  nplayer  game specifies the players' strategy spaces S₁,  S₂,  S₃  S_n  and their payoff function ul, uz, us  un We denote the game by

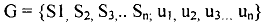
We will  illustrate  the normal form game by a classic example -  The prisoners' dilemma. 

Example: Two suspects are arrested and charged with a crime. The police lack  suff~cient  evidence  to  convict  the  suspects, unless  at  least one  of  them confesses. The police hold  the  suspects  in  two separate cells and  explain  the consequences that will follow from  the actions they could take.  If neither of them confesses then  both will be convicted of a minor offence and sentenced to one month  in jail. If botn of them confess, then both will be sentenced to six months  in  jail. Finally,  if  one confesses  and  the other  does  not, then  the confessor will be  released immediately but the other will be  sentenced to nine months in jail- six for the crime and the other three of obstructing justice. 

The prisoners' problem could  be  expressed  by  a  2x2 matrix. There are two numbers  in  parenthesis  in  each cell  of the matrix,  the  first number  is  the payoff of the prisoner1 and the second one is the payoff of the 2nd  player.  

In  this game 

1)  There are 2 players, two prisoners. 

2)  Strategy set for both the players  is the same S,  = { NC, C), i=1,2. 

3)  The payoff functions of both the players (Prisoner) are described below  

Can  you  solve the problem  of  the  prisoners  and  suggest  them what  is  their optimum strategy  in  such  a  situation. Argue whether that  combination  of strategies  is stable or not. 

Although we stated that  in  a normal form game players chose their strategies simultaneously but  this does not imply that they act simultaneously. It suffices that each player chose her action without the knowledge of the others' choice. Though we said  that in normal form games players move simultaneously, sequential  form games can also be represented in a normal form. But the extensive  form  representation of such  games  is  often  more convenient framework for analyzing such dynamic issues.