Extensive Form Games:

In  the previous section we discussed normal form game, which  is mostly used to represent  static games. Now  we  will  discuss  how  to represent dynamic games. Dynamic games are mostly represented in extensive form. This kind of expositional approach may make it seem that static games must be  represented in  normal  form and  dynamic games must  be  represented  in  extensive form, but  this  is  not  the  case. Any  game  can  be  represented  in  either normal  or extensive  form,  although for  some  games  one  of  the  two forms  is  more convenient to analyse.  

Definition: The extensive form representation of a game specifies

1)  the players in  the game.

2)  a) when each player has to move

b) what each players' choices are when they move

c) the knowledge of each player at each of opportunity to move

3)  the payoff received  by  each player for each combination of moves that could be chosen by the players.

The  contribution  of  extensive  form  representation  is  that games are represented  using games  trees  rather  than words, which  makes  it  easy  and simpler to analyse.

As an example of a game in extensive form consider  the following:

Example: Player  1  chooses an  action a,  from  the  feasible set A₁= {L, R); player 2 observes a, and  then chooses an  action a₂  from  the feasible set A₂= {L, R).  Payoffs of  the  players are u₁  (a₁, a₂) and  u₂  (a₁,  a₂),  as  shown  in  the following game tree

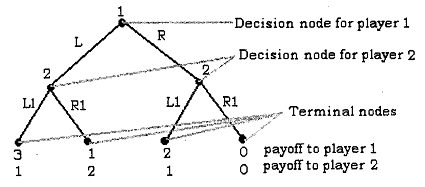
The game tree  begins with  a  decision node for player  1, where  1  chooses between L and R. If  player  1 chooses L,  then a decision node for player 2  is reached, where 2  chooses between L1  and Rl  . Following each of  the player 2's  choices,  a  terminal node  is  reached  (the  game  ends)  and  the players receive their payoffs.

It  is straightforward to extend the game  tree  in  the above figure to represent any dynamic game of complete and perfect information  (that is, any game  in which the  players  move  in  sequence,  all  previous  moves are common knowledge before the next move  is chosen, and the players payoff  from each feasible  combination of moves  are  common  knowledge). Games  with continuous strategy spaces present graphical difficulties, not conceptual.

Dynamic games of incomplete and perfect information can also be represented in  extensive form  (that  is, the games where players do not  know what move was taken by  the others in  the previous step but the payoffs from each feasible combination of moves are common knowledge). For  that we need  to define few terms. Suppose y is a node in an extensive form game and A  (y) is the set of actions available at node y to a particular player. Let us suppose that  in  the previous example, player 2 does not  know what decision has been  taken  by player  1,  that is, player 2 does not know which one of L and R has been taken by  player  I. In  that case, player 2 is not sure in which node she exactly is, she could be  in  the  left node  if player  1 chooses L otherwise in the  right node  if player 1 chooses R. This is called the situation of imperfect knowledge. But as both the players know the payoff that is going to accrue to each of  them  it  is a game  of  complete information.  We  represent  these types of games  in extensive form  in the following way.

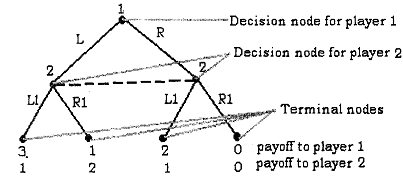
The dotted line  joining nodes of player 2 indicates that player 2 does not know in which node she is. To represent this type of ignorance of previous moves in an extensive form games, we introduce the notion of player's information set.