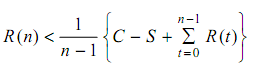Replacement Policy When Money Value Does Not Change With Time

Let us now find the optimal policy for the case of replacement when money value does not change with time.

Let C = capital or purchase cost of new item.

S = scrap or salvage or resale value of the item at the end of 'n' or't' years.

R_n or R (t) = running (or operating) cost for the year 'n' or't'.

n or t = replacement age of the equipment. Here two cases arise

Case I

When time t is continuous variable:

If the equipment is used for't' years, then the total cost incurred over this period is given by

T_c = capital (or purchase) cost - scrap value at the end of t years + running cost for t years.

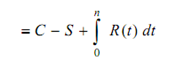
There fore average cost per unit time incurred over the period of n years is

 Equation 1            

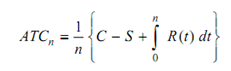
To obtain optimal value of n for which ATC_n is minimum, differentiate ATC_n with respect to n and set the first derivative equal to zero, i.e. minimum of ATC_n.

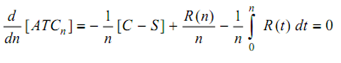
or

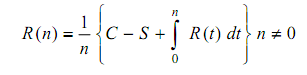
 Equation 2

           R (n) = ATC_n    

Hence the following replacement policy can be derived with the help of Eq. (2).

Policy

Replace the equipment when the average annual cost for n years becomes equal to the current/running cost.

i.e.  Equation 3 

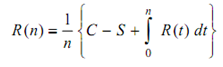
Case II

When time t is a discrete variable :

The average cost incurred over the period n is given by

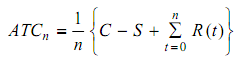
 If C - S and 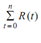  are assumed to be monotonically decreasing and increasing respectively, then there will exist a value of n for which ATC_n is minimum. Thus we shall have inequalities

ATC_{n -1}  > ATC_{n +1}

ATC_{n -1}  - ATC_n  > 0

Rewriting Eq. (3) for period n + 1, we get

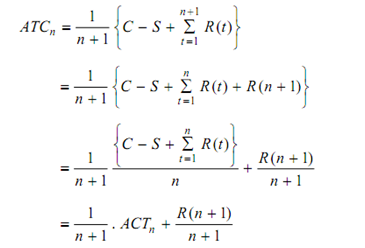
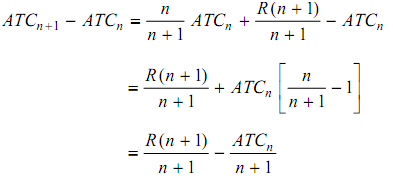
Therefore,

ATC_{n +1 -} ATC_n = (n/ n + 1) ATC_n + (R(n+1) /(n+1)) - ATC_n

= (R (n + 1) / (n+1)) + ATC_n [(n/ (n+1)) - 1]

= R (n + 1) / (n+1) - ATC_n / (n+1)

Since ATC_{n + 1} - ATC_n > 0, we get

R (n + 1)/ (n + 1) - ATC_n  /(n+1)  > 0

i.e.  R (n + 1) - ATC_n > 0

or R (n + 1) > ATC_n

Similarly ATC_{n - 1} - ATC_n > 0 implies that R (n) < ATC_{n - 1}

This provides the following replacement policy.

Policy 1

If the next year, running cost, R (n + 1) is more than average cost of nth year, ATC_n then it is economical to replace at the end of n years

i.e.

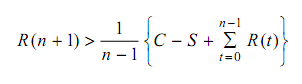
Policy 2

If the present year's running cost is less than the previous year's average cost, ATC_{n - 1} then do not replace.

i.e.