Two-Stage Repeated Games:
In two-stage repeated game, players play the game once again after the payoffs of the game is collected by them. Consider the Prisoners' Dilemma given in normal form in the following table
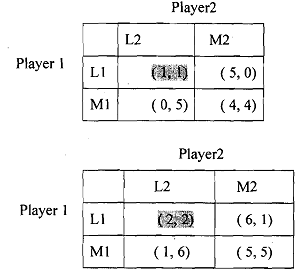
Suppose the players play the game twice, and they observe the outcome of the first game before playing it once again. We further assume that the payoff of the entire game, taking two stages together is simply the sum of the payoffs from the two stages (we assume there is no discounting, that is, the same amount of payoff in any period gives the same amount of utility. Generally, if we think in monetary terms we will prefer Rs. 100 today than Rs. 100 tomorrow. This is because there is a discount rate, which is embedded in our inter-temporal choice decisions).
It is easy to see that the Nash equilibrium of the first stage of the game is (L1, L2) with payoff (1, 1); we have added the equilibrium payoff of the first stage td the payoffs of the game in the next stage. In the second stage also there is a unique Nash equilibrium of the two-stage prisoners' dilemma.