Infinitely Repeated Games:

In  the finite horizon case, the main  focus was that credible threats or promises about future behaviour  can  influence  current  behaviour  and  if there are multiple  IVash  equilibria  of  the stage game,  then  there may be  sub-game perfect  outcomes of  the repeated game G  (T)  in  which, for any  t  < T,  the outcome of  a stage game  is not a Nash equilibrium of G. Whereas  in  case of infinitely repeated games a stronger result is  true. Even if the stage game has a unique Nash  equilibrium, there could  be  sub-game perfect  outcome  of  the infinitely repeated game in which no stage's outcome is a Nash equilibrium of the stage game G.  

An  infinitely repeated game is  an  extension of  a  finitely repeated  game,  it being played  infinitely. Suppose the  prisoners'  dilemma  game is  to  be repeated  infinitely and for each t, the outcome of the t-1 preceding plays of the stage game  is  observed before  the  t'  stage begins. Simple summation of the payoffs  from  this infinite sequence of  stage games does not provide a useful measure of a player's  payoff  in  the  infinitely repeated game. This  is because receiving a payoff 4  is  better  than  receiving a  payoff  1  in every stage but  a summation of the payoff 1, repeated till infinity and that of 4 is same, which is infinity. To tackle this problem, we  introduce the concept of discount rate. As we have argued earlier, Rs. 100  today is not the same as Rs. 100  tomorrow. If the rate of interest is  'r',  one can earn (100xr) one-year later in addition of the principle Rs.  100. Therefore, Rs. 100  today  is worth Rs.  lOO(1 + r)  tomorrow. To  find  the present value of a  future income or future stream of income, we must  discount  it  to get the  present value  of the  future income. To  get the present value  of future  income to  be  received  t  years later we  multiply,  it with 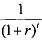 . This fraction  1/(1+r)  is called the discount factor; it  is generally denoted by δ. We can apply this method of calculating the present value of an income  stream to  calculate the  present  value of  the  payoffs of  an  infinitely repeated game.