Finitely Repeated Games:

The argument stated above holds more generally. We  generalise the concept of  repeated  games to games with finite number of repetitions. Let G = (A₁, A₂. ., A_n;  u₁,  U₂,  , u_n)  denote a static game of complete information in which players 1 through n simultaneously choose their strategies a, to a,  respectively from  their  strategy spaces SI  through S,.  This game  is  repeated T times after collecting and observing the outcomes of each game. The game G is called the stage game of  the repeated game.
Definition: Given a stage game G,  let G(T) denote the finitely repeated game in  which G  is  played  T  times,  with  the outcome  of  all  the  previous  games observed before the next play begins. The payoff for G(T)  is simply the sum of the payoffs from the T stage game.

Proposition:  If a stage game G has  a unique Nash  equilibrium then, for any finite  T,  the  repeated game  G(T)  has  a  unique  sub-game perfect  Nash. equilibrium: the Nash  equilibrium  of G  being played  in  every stage  of  the game.

It  is interesting  to investigate if there is more than one Nash  equilibrium in the stage game itself. What will  be  the nature of the equilibrium when the game is repeated? We consider a simple two period game, which  is a simple extension of the prisoners'  dilemma  such  as  there are two  Nash  equilibria  in  it. In addition to the strategies  L1  and  M1,  we  add another strategy  R1  at the  disposal of player  1. Similarly, we add the strategy R2 to the strategy space of player 2. The game is described below  in normal form.

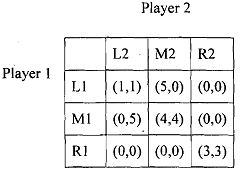
As a result  of adding  the  two  strategies  and  the distribution  of payoffs now there are two pure strategy IVash equilibrium, namely,  (Ll, L2) and (Rl, R2). Suppose the  above  stage game  is  played  twice with  the  first  stage outcome being observed before the second stage begins. Since the stage game has more than one Nash equilibrium,  it  is now  possible for the players to anticipate that different first stage outcomes will be  followed by  different stage game equilibria  in  the  second  stage.  Let  us  suppose  for example the players anticipate that (RI, R2) will be  the second stage outcome if  the  first stage outcome is (Ml, M2),  but  (1,1,  L2) will  be  the second stage outcome  if  any one of  the  eight  other first stage  outcomes  occur.  Thus, the game reduces to the following one shot game, where (3, 3) has been  added to the (MI, M2) cell and (1, 1) has been added to rest of  the cells.

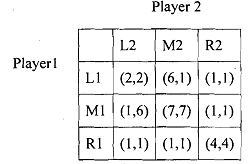
There are three pure strategy Nash  equilibrium of the above game  (Ll, L2), (Ml, M2) and  (Rl, R2). Let us denote  the outcome of the  repeated  game  as [(w, x): (y, z)]; where (w, x) is the first  stage outcome and  (y, z) is the second stage outcome.  Therefore,  the Nash  equilibria namely,  (Ll, L2),  (MI, M2) and (Rl, R2) can be achieved in  the simplified one shot game  if the outcomes of the repeated game are [(Ll, L2), (L1  ,  L2)],  [(Ml, M2); (Rl, R2)] and [(Rl , R2),  (Ll, L2)]  respectively  (if the first stage outcome  is  (Ll, L2), the  second stage outcome has to be  (Ll, L2) according to the players' anticipation and so on for each  of  the one  shot  game's  Nash equilibria).  The  first  and  the  last Nash  equilibria  of  the  repeated  game  are  sub-game  perfect  and  simply concatenate  the Nash  equilibrium  outcome of the  stage game. But  the Nash equilibrium (MI, M2) of the one shot game  is possible  if  the outcome of the repeated game has  the  sub-game  perfect  outcome  [(MI,  M2);  (Rl,  R2]], which means  in  the  first stage,  the  players  chose  (MI, M2) which  is not  a Nash equilibrium of the stage game. We can conclude that cooperation can be achieved in the first stage of a sub-game perfect outcome of a repeated game.

Proposition: We extend this idea to a stage game being played T times, where T is any finite number. If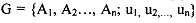 is a static game of complete information with  multiple Nash  equilibria, then  there may  be  sub- game perfect outcomes of the repeated game G(T) in which for any  t< T, the outcome in stage  t is not a Nash equilibrium of the stage game G The main points to extract from the above example is that

• credible threats or  promises about the future behaviour can affect current behaviour
• sub-game perfection  (as we described  in  the previous unit) may not  be  a definition strong enough to embody credibility.