Transformation of variables:

Consider  the earlier example of consumption expenditure, income and wealth. Here the data  is of  the time series format, that is, we have data on the same variables for a number of years or months. One reason for high multicollinearity is that over  time both income  and wealth tend to move together in the data. One way of minimizing this dependence  between the variables is to take thejrst difference of the variables. If the relation is  

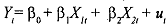
which holds at time t, then it must also hold at time t-1.  Therefore, we have

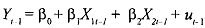
Subtracting equation

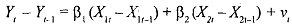
where v_t  = u_t  -  u.  In other words, instead of running the regression on the values of the variables we run them on  the difference between the successive values  of  the  varinbles.  This  reduces the problems associated with multicolliriearity since although X₁ and X,  might be highly correlated  there is no reason to believe that the changes in their levels over time are also highly correlated.

Another transformation that is commonly used  is  the ratio  transformation. Again consider the  earlier model from equation (6.18) above. Let  Y  be consumption expenditure  in  real dollars,  X, be GDP and X,  be population. Since both GDP and population  grow over time they are  likely  to be correlated. One 'solution' is to express the model  in per capita terms, that is, dividing throughout by X,  we get

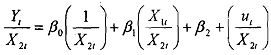
Such a  transformation'mayreduce  collinearity  in the original variables. However, note that the remedy might be worse than the disease. Since it is knom  that the error  term in equation will suffer from problems of heteroscedasticity even when the original errors in are homoscedastic. Similarly,  it is also known that  the  error  term obtained in  the  first difference method v, in equation is going  to be serially correlated even when the original error terms u, were serially uncorrelated.