Pooling of data: 

Another variation of using the apriori information method outlined above  is to combine cross-sectional and time-series data, also known as pooling the data. Consider the following example  -  say you are  interested in studying the demand-for automobiles in  India. Assume you have time series data on  the number of cars sold, average  price of  the car and consumer income. The model specified  is as follows:  

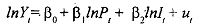
where Y =number of cars sold, P =average price, and I = income and  the subscript  t  is the time period. Our objective is to estimate the price elasticity Pi and  the income elasticity β,  .  In time series data  the price and income variables generally tend to be highly collinear. Therefore, if we run  the  regression given at, we shall be faced with the usual multicollinearity problem. A way out  of this has been suggested by Tobin. He says that if we have cross-sectional data (for example, data generated by consumer panels, or budget  studies conducted by various private and governmental agencies),  we can obtain  a fairly reliable estimate of the income  elasticity β₂ because  in such data, which are at a point of  time, the prices do not vary much. Let  the cross-sectionally estimated income  elasticity be β₂.  Using this estimate we can rewrite  the preceding time series regression as,

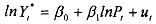
where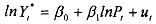, that is, Y represents the value of Y after removing from  it  the effect of income. We can now obtain  an estimate  of the price elasticity from the preceding regression.

This creates a problem of interpretation of the data, because we are assuming that  the cross-sectionally estimated income elasticity  is  the same as  that which would be obtained from the time series data. Nevertheless this technique has been used in numerous studies.