Series System

Suppose a system is composed of two sub-systems say, A and B are connected in series as shown in the figure below. Let the reliabilities of the two components be RA and RB. Now let us compute the reliability say, R of the overall system.

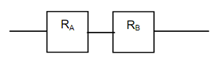
                                                                     Figure: Series System of Two Components

Now, if the probability of failing the sub-systems A and B are denoted by F (A) and

F (B), then we has

R_A = 1 - F (A)             or F (A) = 1 - R_A

R_B = 1 - F (B)             or F (B) = 1 - R_B

We know that there are three possibilities for the system not functioning,

• Sub-system 'A' fails
• Sub-system 'B' fails
• Both Sub-system 'A' and 'B' fail

Thus the system will function only in one case, i.e. if and only if both the sub-systems function correctly.

Thus the probability of A not failing, i.e. 1 - F (A).

And the probability of B not failing, i.e. 1 - F (B).

The probability of both not failing is [1 - F (A)]. [1 - F (B)]

So, the overall reliability of the system R = [1 - F (A)]. [1 - F (B)] = R_A. R_B

Now let us generalize the above concept for N components,

Let N = Number of sub-systems or components of a system connected in series, and

R_K = The reliability or the probability of a component 'K' in the system functioning at a given time, t

R_i = Reliability of the i^th system where i = 1, 2, 3. . . N,

R_s = Reliability of the series system, (i.e. the probability of the system functioning at time t).

The Figure  depicts the series system.

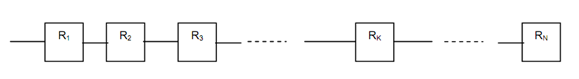
                                                                  Figure: Series System of N Components

The reliability of the above system

R_s = R₁ × R₂ × R₃ × ... × R_k × ... × R_n

It can be discerned that the system fails if any of the sub components fail

 i.e.          R_s = 0, if R₁ or R2 or R3    or ... R_K  ... R_N = 0

 Conversely, if even one element's (components) probability of functioning is improved the whole system's reliability is improved.