Parallel System

Suppose, a system is composed of two sub-systems say, A and B are connected in series as shown in the figure below. Let the reliabilities of the two components be RA and RB. Now let as compute the reliability say, R of the overall system.

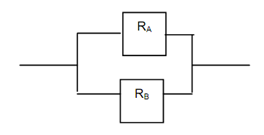
                                                              Figure: Series System of Two Components

Now, if the probability of failing the sub-systems A and B are denoted by F (A) and

F (B), then we have

R_A = 1 - F (A)                or F (A) = 1 - RA

R_B = 1 - F (B)                or F (B) = 1 - RB

We know that there are three possibilities for the components of system not functioning,

• Sub-system 'A' fails
• Sub-system 'B' fails
• Both Sub-system 'A' and 'B' fail

In first and second cases, the system will not completely fail, but only in third case, the system completely fails. Thus, the reliability is affected if and only if both the components fail.

Thus the probability of A failing, i.e. F (A) = 1 - R_A

And the probability of B failing, i.e. F (B) = 1 - R_B

The probability of both failing is F (A). F (B) = [1 - R_A]. [1 - R_B]

Thus, the probability of system not functioning [1 - R_P] = [1 - R_A]. [1 - R_B] So, the overall reliability of the system R_P = 1 - [1 - R_A]. [1 - R_B]

Let us generalise the above concept for N components, A parallel system shown below which 'N' number of elements connected together in Figure has.

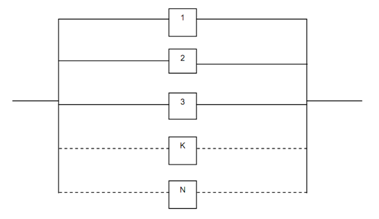
In parallel system if any one component (element) fails, still the system functions. Unless all the components fail simultaneously, the system does function (of course with less power (or capacity)

Let       R_K = Probability of any element 'K' functioning at a given time, t.

Then 1 - R_K = Probability of element 'K' failing in the system.

Also         R_i = Reliability of the i^th system where i = 1, 2, 3, . . . , N.

R_P = Reliability of the Parallel system, (i.e. the probability of the system functioning at time t).

The probability of all the elements failing together

= (1 - R₁) × (1 - R₂) × (1 - R₃) × . . . × (1 - R_K) × . . . × (1 - R_N)

Thus, the probability of a parallel system functioning at a given time t or reliability of the total system of parallel components is,

R_P = 1 - (1 - R₁) × (1 - R₂) × (1 - R₃) × ... × (1 - R_K) × ... × (1 - R_N)