Combined (Series and Parallel) System

It is a combination of series and parallel systems.

In such cases of a system having elements connected both in parallel and series, it is better to convert into one of the systems. Two cases are illustrated as shown below in the Figures 

• Case 1

Here in this case we convert the parallel system into equivalent series system, so that the whole system turns to series type only.

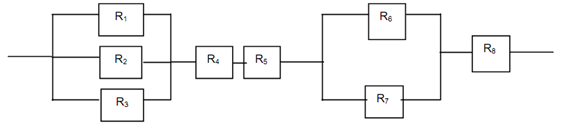
                                                                  Figure:  Combined System - Case 1

In the above system, we consider that we have a series system with (A parallel subsystem of R₁, R₂, R₃), R₄, R₅, (A parallel sub system of R₆, R₇) and R₈, where first, we shall calculate the reliability of the sub systems as follows:

{1 - (1 - R₁) (1 - R₂) (1 - R₃)} = R_x say

And {1 - (1 - R₆) (1 - R₇)} = R_y say

Then the overall system reliability is given by

R = R_x. R₄. R₅. R_y. R₈

= {1 - (1 - R₁) (1 - R₂) (1 - R₃)} R₄. R₅. {1 - (1 - R₆) (1 - R₇₎. R₈}

• Case 2

Consider the case of combined system as shown in Figure 9.8. In this case it is better to convert the components into equivalent parallel system. Here we shall consider the three subsystems as parallel. The top sub system and bottom subsystems are having the components in series. Thus we consider as a parallel system of (A series subsystem of R₁, R₂), R₃ and (A series subsystem of R₄, R₅, R₆).         

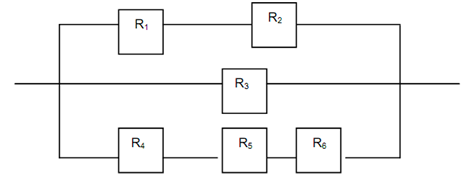
                                                                   Figure: Combined System - Case 2

Thus the overall reliability can be computed as

For series subsystem of R₁, R₂, it is Say R_x = R₁ × R₂

For series subsystem of R₄, R₅, R₆, it is Say R_y = R₄ × R₅ × R₆

The overall System reliability is

R = 1 - (1 - R₁ × R₂). (1- R₃). (1 - R₄ × R₅ × R₆)

= 1 - (1 - R₁ × R₂). (1-R₃). (1 - R₄ × R₅ × R₆)