Spatial Curvature:

Assume that you are in a space ship traveling via deep space. The ship's rockets are fired up, and the vessel accelerates at a tremendous rate. Assume that the laser apparatus is in the ship, though rather of a mirror on the wall reverse the laser, there is a screen. Before the acceleration starts, you align the laser and hence it shines at the middle of the screen (as shown in figure below). What will occur whenever the rockets are fired and the ship accelerates?

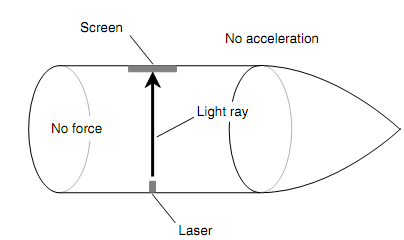
Figure: As seen from inside the ship, the laser beam travels in a straight line across the vessel whenever it is not accelerating.

In a real-life situation, the spot from the laser will not move on the screen sufficient for you to observe. This is so since any reasonable (i.e., non-life-threatening) rate of acceleration will not cause enough force to affect the beam. Though, let us suspend our doubt and visualize that we can accelerate the vessel at any rate, no matter how great, without being compressed against the ship's rear wall. When we accelerate fast sufficient, the ship pulls away from the laser beam as the beam travels across the ship. We, are looking at the circumstances from within the ship, see the light beam obey a curved path (as shown in the figure below). The stationary spectator on the outside sees the light beam follow a straight path, though the vessel pulls out ahead of the beam (as shown in the figure below).

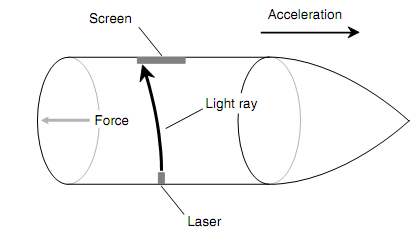
Figure: As seen from inside the ship, the laser beam travels in curved path across the vessel whenever it is accelerating at a high rate.

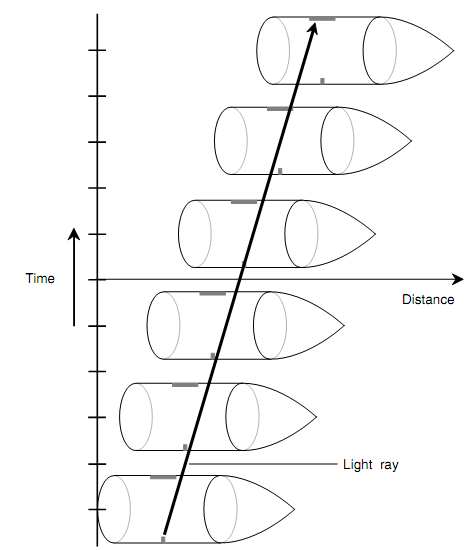
Figure: Whenever seen from a "stationary" reference frame exterior the ship, the accelerating vessel pulls away from the straight-line path of the laser beam and hence it strikes the screen off-center.

Despite of the reference frame, the ray of light always obeys the shortest possible path among the laser and the screen. Whenever seen from any non-accelerating reference frame, the light rays emerge straight. When noticed from accelerating reference frames, though, light rays emerge curved. The shortest distance among the two points at opposite ends of the laser beam in the figure above is, in fact, curved. The apparently straight path is in actuality longer than the curved one, as viewed from inside the accelerating vessel! It is this phenomenon which has led some people to say that "space is curved" in an influential acceleration field. Since of the principle of equivalence, the powerful gravitation causes similar spatial curvature.

For spatial curvature to be as observable as it emerges in both figures shown above, the vessel should accelerate at a tremendously large pace. The standard unit of acceleration is the meter per second per second, or meter per second squared (m/s²). Aerospace engineers and astronauts also state acceleration in units termed as gravities (denoted by g), where one gravity (i.e., 1 g) is the acceleration which generates the same force as the gravitational field of the Earth at the surface, around 9.8 m/s². (Do not confuse the abbreviation for gravity or gravities with the abbreviation for grams! Pay concentration to the context when you see a unit denoted by g.) The drawings of both figures show the condition for an acceleration of many thousands of gravities. When you weigh 150 pounds on Earth, you will weigh a lot of tons in a ship accelerating at a rate, or in a gravitational field of such intensity, therefore as to cause that much spatial curvature.

Is this a simple academic exercise? Are there really gravitational fields powerful sufficient to "bend light rays" appreciably? Sure. They exist near to the event horizons of the black holes.