Point of View:
Assume that there are eight clocks in space set at the vertices of a huge cube. Each edge of the cube measures 1 light-minute, or around 1.8 x 107km (i.e., 1.1 x 107mi), long, as shown in figure below. We are provided a challenge: Synchronize the clocks, therefore they agree in the limit of visibility, let say, to within 1 second of each other. Do you assume that this will be simple!
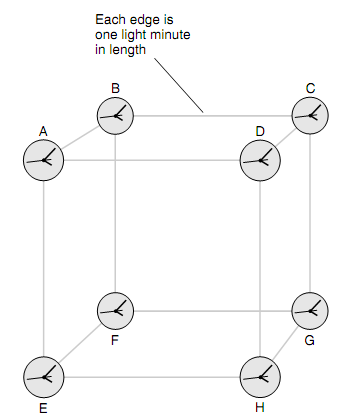
Figure: A hypothetical set of eight clocks set at the vertices of a cube which measures 1 light-minute on each edge. How will we synchronize such clocks?
Since the clocks are so far distant, the only manner we can ascertain what they state is to equip them with radio transmitters which send time signals. Alternatively, when we have a powerful sufficient telescope, we can notice them and read them directly by vision. In either situation, the information which tells us what the clocks state travels to us at the speed of light. We acquire in our space ship and maneuver ourselves therefore we are in the precise center of the cube, equidistant from all the eight clocks. Then we continue to synchronize them by using remote-control, wireless two-way data communication tool. Thank heaven for the computers! The task is proficient in just a few minutes. It cannot be completed instantly, obviously, as our command signals take the better portion of a minute to reach the clocks from our central position, and then the signals coming back from the clocks take just as long to acquire to us and hence we can see what they state. Soon, though, everything is in agreement. The clocks A via H all tell the same time to in a fraction of a second.
Pleased with our work, we cruise out of the cube. We receive a look back at the clocks. What do we view? The clocks have already managed to get out of the sync. We take our ship back to the middle of the cube to accurate the problem. Whenever we get there, though, there is no problem to correct! The clocks are all in agreement all over again.
You can estimate what is occurring here. The clock readings based on how far their signals should travel to reach us. For a spectator at the middle of the cube, the signals from all eight clocks, A via H, arrives from exactly the similar distance. Though, this is not true for any other point in space. Hence, the clocks can be synchronized only for which one favored point; when we go anywhere else, we will have to synchronize them over again. This can be completed, though then the clocks will be synchronized only whenever noticed from the new favored vantage point. There is an exclusive sync point-the spot in space from which all the eight clocks read similar-for each coordination of the clocks.
No sync point is more suitable than any other from a scientific viewpoint. When the cube occurs to be stationary associative to some favored reference point like the Earth, we can synchronize the clocks, for ease, from that reference point. Though, when the cube is moving associative to our frame of reference, we will never be capable to remain the clocks synchronized. The time depends on where we are and on whether or not we are moving associative to whatever device we use to point out the time. The time is not absolute, though relative, and there is no getting about it.
PROBLEM:
Assume that there is an atomic clock on the Moon (i.e., clock M), and its time signals are broadcast by a very powerful radio transmitter. This clock is set to exactly agree with the other atomic clock in your home town on Earth (i.e., clock E), and it is also equipped with a radio transmitter. When you travel to the Moon, what will be the associative readings of the two clocks, as established by listening to the radio signals?
SOLUTION:
The Radio signals travel via space at around 3.00 x 105 km/s. The Moon is around 4.0 x 105 km, or 1.3 light-seconds, away from the Earth. The reading of clock M will be shifted around 1.3 s ahead in time (i.e., earlier) since the time lag for its signals to reach you will be removed. The reading of clock E will be shifted around 1.3 s behind in time (i.e., later) since a time lag will be initiated where earlier there was none. Whenever you get to the Moon, the clock M will be around 2.6 s ahead of the clock E.