Observational Confirmation:

When Einstein invented his universal theory of relativity, a few of the paradoxes inherent in special relativity were solved. (Such paradoxes have been ignored here as discussing them would only confuse you.) In specific, light rays from far-away stars were noticed as they passed close to the Sun to view whether or not the Sun's gravitational field, that is quite strong close to its surface, would bend the light rays. This bending would be noticed as a change in the apparent location of a far-away star in the sky as the Sun passes near to it (as shown in figure below).

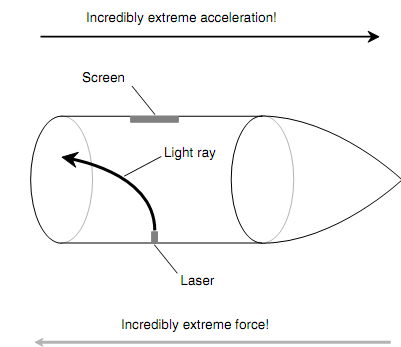
Figure: When the acceleration is great sufficient, the spatial curvature becomes extreme.

The problem with this kind of observation was, as you may guess, the fact that the Sun is much brighter than any other star in the sky, and the Sun's light generally washes out the faint illumination from far-away stars. Though, during a total solar eclipse, Sun's disk is occulted by the Moon. In adding up, the angular diameter of the Moon in the sky is nearly precisely the same as that of the Sun; therefore light from far-away stars passing near to the Sun can be viewed by earthbound spectators during a total eclipse. Whenever this experiment was carried out, the apparent location of a far-away star was certainly offset by the presence of the Sun, and this effect occur to the similar extent as Einstein's general relativity formulas said it must.

More lately, the light from a certain quasar has been noticed as it passes near to a suspected black hole. On its approach to us, the light from the quasar obeys multiple curved paths about the dark, huge object. This generates several images of the quasar, set further or less in the form of a "plus sign" or "cross" with the dark object at the middle.

The curvature of space in the company of a strong gravitational field has been likened to a funnel shape (as shown in figure below), apart from that the surface of the funnel is 3-dimensional instead of 2-dimensional. The shortest distance in 3-dimensional space among any two points close to the gravitational source is all the time a curve with respect to 4-dimensional space. This is not possible for most people to visualize directly without "cheating" by taking away one dimension. The mathematics is clear-cut sufficient, however, observations have shown that it properly elucidates the phenomenon.

Figure: Spatial curvature in the vicinity of an object which generates an intense gravitational field.