Laser Clock:

Assume that we have a space ship prepared with a laser/sensor on one wall and a mirror on the opposite wall (as shown in figure below). Suppose that the laser/sensor and the mirror are located therefore the light ray from the laser should travel perpendicular to the axis of the space ship, perpendicular to its walls, and (once we obtain it moving) perpendicular to its direction of the motion. The laser and mirror are adjusted therefore they are estranged by 3.00 m. Since the speed of light in air is around 3.00 x 10⁸ m/s, it takes 1.00 x 10^-8 s, or 10.0 nanoseconds (i.e., 10.0 ns), for the light ray to acquire across the ship from the laser to the mirror and the other 10.0 ns for the ray to return to the sensor. The ray hence needs 20.0 ns to make one round trip from the laser/sensor to the mirror and return again.

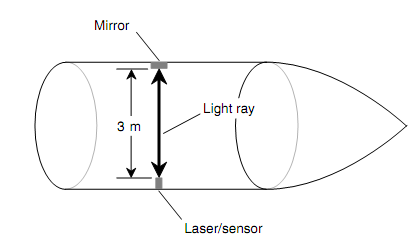
Figure: A space ship prepared with a laser clock. This is what an spectator in the ship always notices.

Our laser releases pulses of very brief duration, far shorter than the time needed for the beam to acquire across the ship. We may even assume that the beam releases just a few photons in each burst! We measure the time increment by using an tremendously sophisticated oscilloscope therefore we can observe the pulses going out and coming back and measure the time lag among them. This is an exceptional clock; its timekeeping capability is based on the speed of light that Einstein proposed is constant no matter from which point of view it is observed. There is no superior way to remain time.