Clock In Motion:
Suppose now that we are exterior to the ship and are back on Earth. We are prepared with a special telescope which permits us to see in the interior of the ship as it whizzes by at an important fraction of the speed of light. We can view the laser, the mirror, and even the laser beam itself since the occupants of the space vessel comprise temporarily filled it with smoke to make the viewing simple for us. (They have pressure suits on therefore they can breathe.)
What we view is depicted in figure shown below. The laser beam yet travels in straight lines, and it still travels at 3.00 x 108 m/s associative to us. This is true since of Einstein's axiom regarding the speed of light and the fact that light rays always emerge to travel in straight lines as long as we are not accelerating. Though, the rays have to travel beyond than 3.00 m to acquire across the ship. The ship is going too fast that by the time the ray of light has arrived at the mirror from the laser, the ship has moved a major distance forward. The similar thing occurs as the ray returns to the sensor from the mirror. As an outcome of this, it will appear to us, as we look at the ship from the Earth, to get more than 20.0 ns for the laser beam to go across the ship and back.
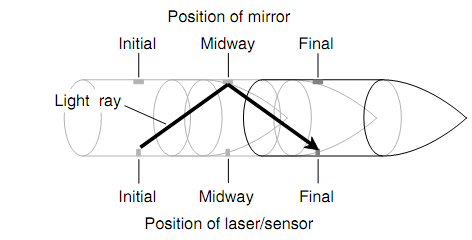
Figure: This is what an exterior observer views as the laser clock equipped space ship whizzes by at a sizable fraction of the speed of light.
Since the ship goes by, time emerges to slow down within it, as view from a "stationary" point of view. Within the ship, though, time moves at normal speed. The faster the ship goes, the bigger is this inconsistency. As the speed of the ship approaches the speed of light, the time dilation feature can become large certainly; in theory, there is no boundary to how great it can become. You can imagine this by imagining the figure shown above stretched out horizontally therefore the light rays have to travel nearly parallel to the direction of motion, as view from the "stationary" reference frame.