Velocity in a Moving Frame of Reference:

Assume a body performing plane motion as illustrated in Figure. This body can be a vehicle. OX and OY axes are the fixed axes. If I and J are unit vectors along them respectively, then we may say

dI / dt = 0,                      dJ/ dt  = 0

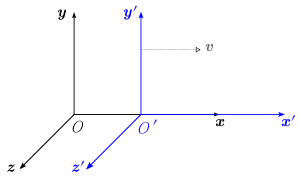
Let any particle P (say, presently at B) that is moving in the vehicle itself. Furthermore, let us consider any one point A as pole in the body. Then motion of P may be studied by fixing axes A_x and A_y to the vehicle at A, i and j are unit vectors working along A_x and A_y respectively. These axes also rotate along the vehicle and therefore we can say di/ dt and dj / dt exist. Also ω and α are the absolute angular velocity & acceleration of the body.

If       

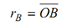
Then

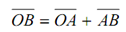
Or

r_B  = r_A  + r_{A B}

 These vectors also may be expressed with reference to fixed set of axes, as below,

r_B  = X _B  I + Y_B  J

r_A  = X _A  I + Y_A  J

and

rA B  = X P  i¯ + YP   j¯

∴ d r_B /dt =  d / dt ( X_B I¯ + Y_B  J¯)

=  d/ dt (X _A  I + Y_A  J ) + d/dt ( X _B  i + Y_B   j)

= d X _A/dt  I  + d Y_A / dt  J + X _B  di/dt + YB dj/ dt + i d X _B/ dt  + j d Y_B/ dt

 but

 di/ dt = ω × i dt      and  dj / dt = ω × j

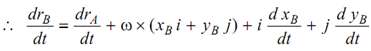
∴ dr_B/ dt = dr_A/dt + ω × ( x_B i + y_Bj) + i d x_B /dt+  j d y_B / dt

 ∴ v_B  = v _A  + v _AB  + v_Br