Relationship between E and G:

Below figure shows what is known as the state of pure shear. The deformation of the body because of the shear is shown in Figure (projected view).

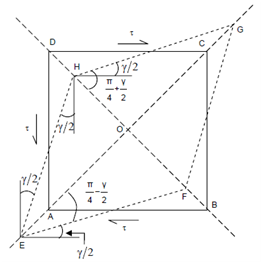
Figure

The state of stress on the element is given by the stress component S, τ_xy =- τ _yx  = τ . Due to shearing strain the original plane ABCD (a square) gets distorted into a rhombus EFGH. The magnitude of the shear strain γ is given by change in the right angles ∠ BAB, ∠ ABC, ∠ BCD and ∠ CDA. This change is produced by rotations of pairs of lines by γ/2 such as ∠ DEH.

Using Eqs. (31) and (32), let us find the stress components on the diametral planes DB and AC whose aspect angles are π/4 and 3π/4 respectively. On plane DB, we get

Normal stress component, σ = τ sin 2θ

= τ sin (2π /4) = τ

Shear stress component      = τ cos 2θ

= τ cos            (2π/4)= 0

Similarly, on plane AC,

Normal stress component = τ sin 2θ

=τ cos 2π/4 = 0

Shear stress component      = τ cos 2θ

=τ cos 2 × 3 π/4= 0

Hence, the distortion of the square ABCD by shear stress may also be treated as due to the elongation of the diagonal AC due to normal stress of + τ on planes parallel to BD and shortening of the diagonal due to normal stress of - τ on planes parallel to AC.

 ε_OA =  (τ/E) -v(-τ/E)  = τ (1 + v)/E

ε_OB =  -(τ/E) -v(τ/E)  = -τ (1 + v)/E

OE =OA (1+ε_OA)

OF =OB (1+ε_OB)

Φ = OEF = π/4 - γ/2

tan Φ = tan (π/4 - γ/2) = 1- (γ/2)/ 1+ (γ/2)

From Figure,

 tan Φ = OF/OE = OB (1 + ε_OB )/ OA (1 + ε_OA ) = OB (1 + ε_OB )/OB (1 + ε_OA ) (Q OA = OB)

tan φ= (1 - τ (1 + v)/E)/(1 + τ (1 + v)/E)

On comparing Eqs. (37) and (38),

γ/2 =  τ/E (1 + v)

or shear strain  γ= (2 τ (1 + v))/E

Rigidity Modulus   G = Shear stress/ Shear strain = τ/(2τ (1 + v)/E)

G =      E/2 (1 + v)