Markov Analysis

In hierarchical scheme, routes for the worker, which is the promotion ladder, are well defined. It means every worker elevates himself in the organisation by a well distinguish career path. All of the employees begin in an organisation at the bottom rung and climb the ladder one at a time. Any kind of wastage is falling off the ladder. Young and Almond (in year 1961), devised a hierarchical manpower schema, framing sub-groups on the basis of length of service and salary grade. They have utilized the theory of the Markov process to calculate the long-term equilibrium distribution of staff between the sub- groups. The basic supposition of this model is that worker in a specific grade or a status group has a fixed possibility of promotion in a given year, independent of vacancy. Therefore number receiving promotion based on the number of qualified staff in the grade below, subject to fulfilment of eligibility criteria, which may be, seniority, age, qualifications or experience. The central equation for this model is following:

                                                       n (t + 1) = n (t) P + R (t+1)r

            Where, n (t) = the vector of stocks at a given time t, for example. number of employees in each status group.

  P =          the matrix of transition probabilities among each of status groups.

  r =          the vector of probabilities of a recruit beginning in particular status groups.

R (t) =    the number of new recruits at time t.

If the number of workers n (t) in each of the status group at a specific time is known, the equation can be used to predict the value of n (t), for example number of employees in each status group at a later time t. However, this is subject to the conditions that recruitment levels, for example: R (t) during the period, for example. t = 0 to t = T, are already known or specified. On the other hand, the overall number of staff in the system, which is N (t) can be specified. The prediction equation, therefore, can be rewritten in the following outline.

                            n (t + 1) = n (t) q + m (t + 1) r

It is the more usual form of the Markov chain model than the earlier one. In this, M (t +1) = N (t+1) and includes transition within the organisation and also the effects of wastage and recruitment to maintain the balance in the organisation. HRP via Markov Chain is considered mere probabilistic. Moreover, Markov models permit too many fluctuations of the sizes of the status group, when in practice sizes are tightly constrained. To ignore such difficulty the renewal theory of HRP was developed.  

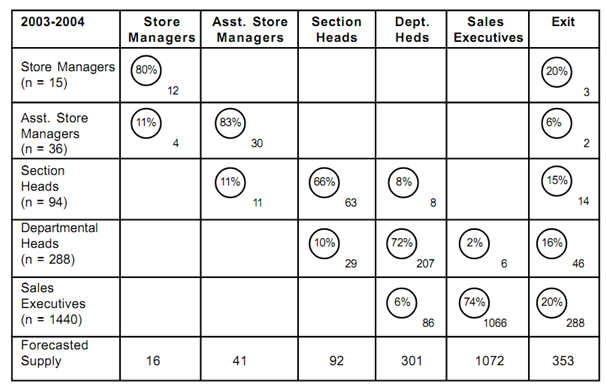
                 Fig: Estimated Internal Labour Supply for a given Firm