Work Of Compression In Steady Flow
The equation of the steady flow energy per unit mass for the compression process, supposing that modifications in kinetic and potential energy are negligible might be written (as refer to figure shown below).
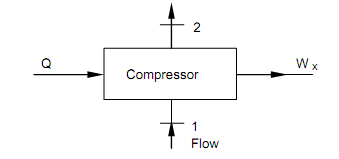
Figure: Steady Flow Process
Q – Wx = Δh = h2 – h1
We have a relation T ds = dh – v dp for a reversible procedure.
Q = Δh - ∫ vdp
Then for any of the ideal conditions of figure shown above from the above two equations,
Wx = - ∫ vdp
For any of the gas a compression procedure might be symbolized with sufficient accurateness by an equation like pvn = constant.
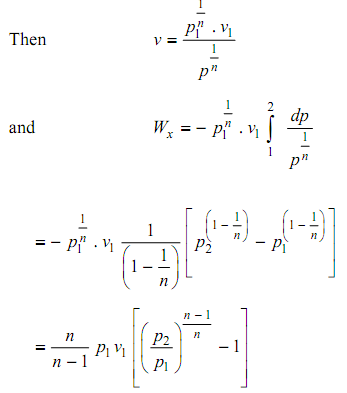
The work of compression or steady flow work input to the gas is negative of the shaft work Wx.
And hence, Wn = Work of reversible polytropic compression
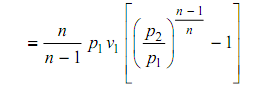
Wγ = Work of the reversible polytropic compression
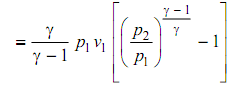
For isothermal compression of an ideal gas, pv = constant. The work done of reversible isothermal compression is,
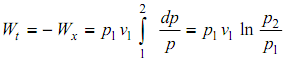
in the p – v plot of the figure shown above, the work of compression for each kind of procedure is symbolized by the region among the path of that procedure and the axis of pressure. It is evident that the work of reversible isothermal compression is low than the work of reversible adiabatic compression; the work of reversible polytropic compression is intermediary among the others when n lies among γ and unity. This is the condition in actuality as the polytropic condition will include some cooling though not sufficient to acquire isothermal compression. In an actual compressor the work will be larger than the work of the reversible compression procedure since of friction. In such conditions the path of compression might be symbolized by pvn = constant, though the work of compression is not specified by ∫ vdp; the shaft work cannot be established solely from the properties of the fluid. The friction effect in a reciprocating compressor is frequently small and hence the work may be calculated by the integral of ∫vdp without big error.