Minimum Work In Two Stage Compression With Intercooling

The circumstances affecting the work of compression might be studied by the use of steady flow system and T–s diagram of the figure shown below. As illustrated in the figure, an ideal gas is compressed from the preliminary state p₁ T₁ to p_x, it is then chilled at constant pressure to T_y, and then compressed from p_x, T_y to p₂. Specified p₁, T₁, Ty and p₂, it is preferred to compute the value of px that gives lowest work.

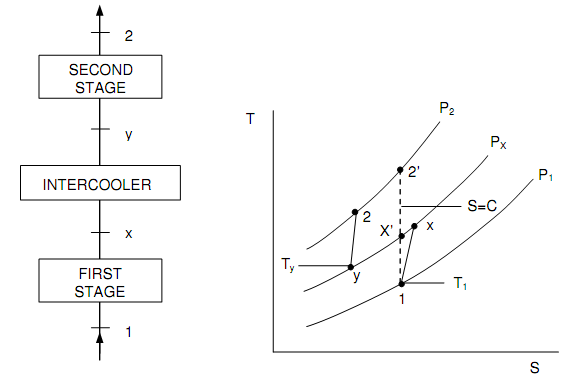
                                            Figure: T – s Plot of Two-stage Compression procedure

Let assume the adiabatic compression efficiencies of the two-stages be correspondingly η_c1 and η_c2.
The work of compression

                                                                   w_c = w₁ + w₂

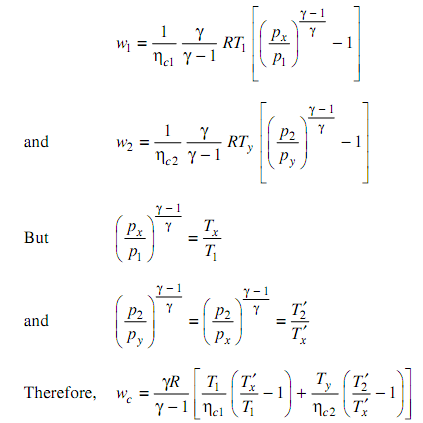
On taking the derivative with respect to Tx′ and setting it equivalent to zero (noting that, T₁T₂′ and T_y are constant,
                                                                 dw_c/dT’_x = 0

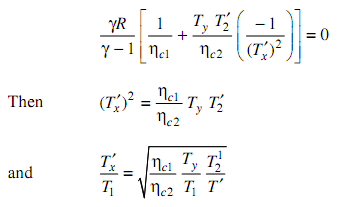
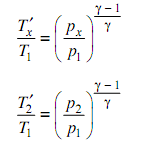
Hence, for minimum work in two phase compression of a perfect gas with inter-cooling to a fixed temperature T_y,

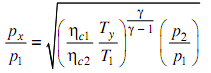
For special condition of T_y = T₁ and η_c1 = η_c2, which is frequently taken as standard of comparison, the need for minimum work is

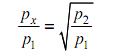
Also for this special situation the condition of minimum work is the condition of equivalent work in the two phases.

Whenever three phases of equivalent effectiveness are employed, with inter-cooling to the preliminary temperature at two points as shown in figure below, the condition of minimum work and of equivalent division of work among phases is,

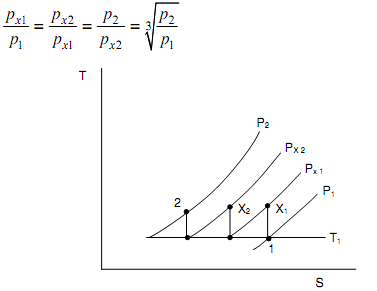
                                           Figure: Three-phase Compression with Inter-cooling