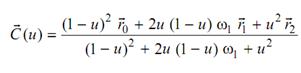Rational quadratic curves-conic sections:

In this case

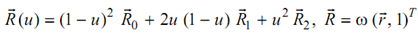
With        ω(u) = (1 - u)²  ω₀ + 2u (1 - u) ω₁ + u ² ω₂

Therefore

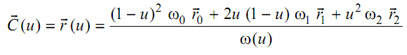
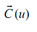lying in the convex hull of is a plane curve. Also  is a general quadratic; with appropriate choices of the vectors

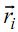and weights w_i , it may represent any conic segments exactly.

First of all, if ω_i → k ω_i (k ≠ 0), C (u) remains the similar.

Secondly, let

u =       1 / (p (1 - t ) + t ) , 1 - u = p (1 - t ) / p (1 - t ) + t

then

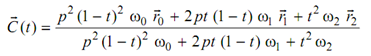
Thus the shape is not changed if ω_i → p ^{2 - i} ω_i = ωˆ _i .

 In particular, choose  p =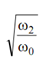, then 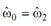. Therefore all C (u) with ω₀ , ω₂ ≠ 0

may be transformed into 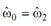=1