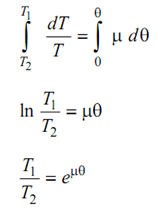Flat Belt:

Assume tension on the tight side is 'T₁' and the tension on the slack side is 'T₂'. Assume 'θ' be the angle of lap and 'μ' is the coefficient of friction among the belt and the pulley. Assume an infinitesimal length of the belt PQ that subtends an angle δθ at the centre of the pulley. Assume 'R' be the reaction among the element & the pulley. Consider 'T' be tension on the slack side of the element that is at point P and assume '(T + δT)' be the tension on the tight side of the element.

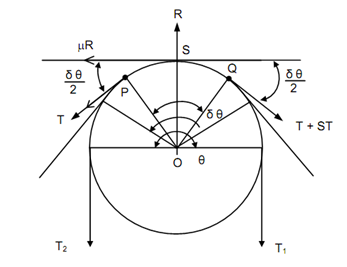
The tensions T & (T + δT) will be applying tangential to the pulley and so normal to the radii OP & OQ. The friction force will be equivalent to 'μR' and its action shall be to prevent slipping of the belt. The friction force shall act tangentially to the pulley at the point S.

Resolve all of the forces in the tangential direction

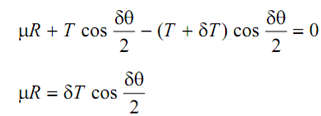        . . . (8.6)

Resolving  out all the forces in the radial direction.

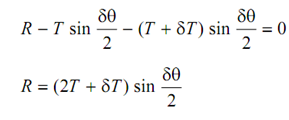
As δθ is very small, by taking limits

∴     

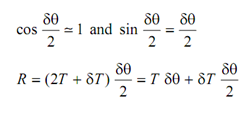
Neglecting the product of the two infinitesimal quantities 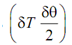  that is negligible in comparison to other quantities:

∴  R ≡ T δθ

Substituting the value of R and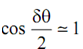in Eq. (8.6), we obtain

μT δθ = δT

or,

δT/T  = μ δ θ

By Taking limits on both of sides as δ θ → 0

dT/T = μ d θ

Integrating among limits, it becomes