Non-Equilibrium in Mass Transfer Term (Cu):

This term in nonideality arises due to the fact that equilibrium in the distribution of the solute among the stationary and the mobile phases cannot be attained because the mobile phase is continuously moving. If here the Conc._L and Conc._G are the concentrations of the solute in the liquid and gas phases, correspondingly and if we apply Henry's law to give the following expression:

Conc._L  / Conc._G = K

or, Conc._L= K.Conc._G

But Henry's law is valid in equilibrium condition and for cases where insufficient time is available for equilibration, we could write

Conc_L= K Conc_G  × f(t)

where, f(t) is some function of time which reflects the kinetics of mass transfer process between the two phases. If t is extremely large, that is when equilibrium is approached, f(t) approaches unity and the validity of Henry's law is observed. In the actual situation the equilibrium is not instantaneous and band broadening is observed. Figure shows the ideal and non ideal conditions in the solute distribution between the two phases.

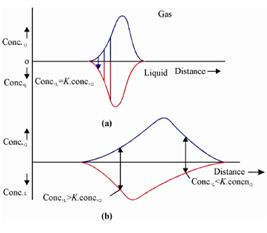
Figure:  Concentration profiles of a solute in gas and liquid phases (a) Instantaneous equilibrium leading to ideal distribution (b)    Finite rate of mass transfer leading to actual distribution

Figure (a) depicts where equilibrium is attained in all the plates before mass transfers are made. Figure (b) depicts where gas is continuously moving and equilibrium is never attained and in general, Conc._L≠ K Conc._G. Initially, the front of the solute zone in the gas encounters some of the solute dissolved in the liquid and we do not wait for the equilibrium to be established; thus, conc._L<conc._G. At the other extreme end of this plot, a rear of the gas phase solute zone, a solute is unable for leave the liquid rapidly sufficient to equilibrate with the fresh carrier gas and Conc._L> K.Conc._G. This means that a part of the solute is retained more in the liquid phase than would have if the equilibrium was established instantaneously. This process continues through the length of the column and the peak is broader than would have actually been observed.