Statistical Aspects of Radioactivity:

Any scientific measurement is subject to error and so is true about radioactivity measurement. In general, these may be of two types; systematic or determinate and random or indeterminate errors. The latter type cannot be eliminated but can be evaluated by statistical methods as these are random in nature. Radioactive decay is a random phenomenon and its measurements are governed by the laws of statistics.  It is different from normal analytical measurements where reproducibility is essential whereas in case of radioactivity it is not so. For example, you should not get, the same counts in a repeated measurement unlike in all other measurements where reproducibility is a must. It has added advantage in that it can be used to check a counting system, if it is working correctly or not. In radioactive decay each atom has a certain probability of decay within any time interval. When a radioactive sample is counted then it is possible to calculate the probability of count rate within certain limits of the true or average count rate. Every count 'n' has inherent error of ± √n and thus count rate should always be represented by n ± √n. The probability can be correctly expressed by binomial distribution law but it is a common practice to use Poisson distribution law according to which probability of occurrence of value n, P (n) can be expressed as:

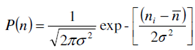
where n_i = measured count at any time,

     = average of the measured counts and

σ = standard deviation expressed as;

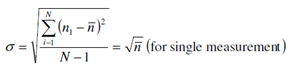
where N is the number of measurements. If the error in the count rate is measured then

σ_R = √n/t

where, t is the time interval of counts collected. The probable error expresses the limits within which 50% probability exists for the occurrence of true value.

P = 0.67σ = 0.67  √n

Since σ is so easy to calculate, it is used most frequently to express the error of a measurement. However, it is helpful to know that the probability of error decreases with the number of standard deviations. Such calculations make it possible to establish a Rule of Thumb for the rejection of unlikely data beyond .