Logic Circuit after K-map Simplifications:

An octet may be visualized as two adjacent quads (refer to Figure (a)), this is a group of 8 adjacent 1s and it leads to removal of three variables and their complements. Let us assume the SOP equation for the octet of Figure (a) and simplify this.

Y = A¯B (C¯ D¯ + C¯D + CD + C D¯) + AB (C¯ D¯ + C¯D + CD + C D¯) = A¯B + AB

= B ( A¯ + A) = B

Which leads to removal of three variables C, D, A and their complements? Thereby from this simplification of the K-map the logic circuit for this specific SOP equation shall have only one input B rather than four variables as illustrated in Figure (b).

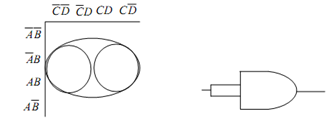
(a)                                                   (b)

Figure: (a) Rectangle Adjacent 1s Octet in K-map, and (b) Logic Circuit after K-map Simplifications

Overlapping Groups

In case of overlapping groups we may use same 1 more than once in forming adjacent groups of 1s as represented in Figure (a). The SOP equation for the case of overlapping groups of Figure (a) after doing Karnaugh simplifications is

                                                              Y = B + C D¯ A