No Equilibrium in Pure Strategy:
Each of the games we have considered so far has had at least one Nash equilibrium in pure strategies. But there could be games in which there is not a single pure strategy Nash equilibrium. Consider the following example of constant sum game (the constant sum of payoffs being 100).
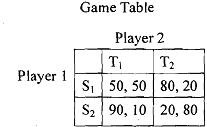
We will try to find the solution (Nash equilibrium) of the game by trial and error method. We will take each possible combination of strategies and investigate whether that survives the condition of Nash equilibrium, as there is no strictly dominated strategy.
Case I: (S1, T1)-> If player 1 adopts the strategy S1, player 2 will choose TI (this is because when player 1 chooses S1, playing T1 fetches her 50, whereas playing T2 fetches 20 only). Thus, given the equilibrium strategy of player 1 to be S1, player 2 is doing her best. But if player 2 chooses T1, player 1 will choose S2 (why?). Thus, the strategy vector (S1, T1) is not self-enforcing. To be specific, player 1 has no incentive to stick to this equilibrium. Therefore, (S1, T1) cannot serve as a Nash equilibrium.
Similarly, we can show that none of (S1, T1), (S1, T2), (S2, T1) can serve as a Nash equilibrium of the game.