Degree-p B-spline curve:

A degree-p B-spline curve is described as :

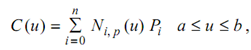
where, {Pi} are the n control points,

{N_{i, p} (u)} are degree -p B-spline basis functions over the knot vector along m intervals U = {a, . . . , a, u_{p + 1}, . . . , u_{m - p - 1}, b, . . . , b}

(i) Extreme values, a and b, are repeated (p + 1) times each. There are (m + 1) knots.

(ii) In general, the knot vector is non-periodic & non-uniform.

As previous, we list some 'nice' properties of B-splines, before going through some instance.

(i) If n = p, & U = {0, . . . , 0, 1, . . . , 1}, then C (u) is a Bezier curve.

(ii) For curve of degree p, along (n + 1) control points and (m + 1) knots, m = n + p + 1.

(iii) For a ≤ u ≤ b, C (a) = P₀, and C (b) = P_n.

(iv) Affine Invariance : Affine transformations of the coordinate system do not alter the shape of the B-spline curve. 

(v) Strong Convex Hull Property :

          a) The curve is contained in the convex hull of its control points.

          b) If ui î_ X Xi + 1, and p î_ L _P - p - 1, then C (u) is contained in the convex hull of the control points P_{i - p}, . . . , P_i.

          c) This result may be derived from the non-negativity and partition of unity properties of the basis functions.

(vi) Local Modification: Moving P_i alter C (u) just in the interval [u_i, u_{i + p + 1}), as outside this interval, N_{i, p} (u) = 0.

(vii) A B-spline of degree-1 is identical to the control polygon. Since the degree of the B-spline is lowered, it comes closer and closer to the control polygon.