Consequences and Derivatives:

(a)   Enhancing the degree, p, of a B-spline curve increases its continuity.

(b)   Enhancing the knot multiplicity reduce the continuity.

    Derivatives: The following formula describes the k-th derivative of N_{i, p} (u) in terms of the k-th derivatives of the basic functions of N_{i, p - 1} (u) and N_{i + 1, p - 1} (u). It might be utilized to compute all of values of derivatives for a provided value of u.

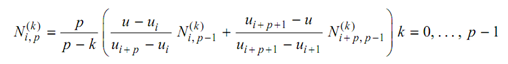
The above formula decreases the k-th derivatives of a degree-p basis function in terms of the k-th derivatives of degree p - 1. Two other computationally useful forms are the following two:

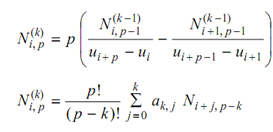
where  a_{0, 0} = 1,

a _{k, 0} =  a_{k -1, 0} / u _{i + p - k +1} - u_i

ak, j =   a_{k -1, j}  - a_{k -1, j -1}   /  u_{i + p + j - k + 1} - u_{i + j}    when  j = 1, . . . , k - 1

a_{k, k} =  - a_{k -1, k-1}  /( u_{i + p +1} - u_{i + k} )

In the last form, while computing the ai, j's, if the denominator = 0, the expression is described to have value = 0. All derivatives k > p are zero (the curve is of degree p).

The lowest & the highest knot values are known as the extreme values of the knots. All of other values of knots are called as interior values. If all of interior knots are spaced consistently among the extreme values, the resulting B-spline is called as a uniform B- spline. Or else, it is called as Non-uniform B-spline (NUBS).