Gibbs-Dalton Laws:

Dalton's Law of Partial Pressures

Let a homogeneous mixture of non-reacting ideal gases 1, 2, etc., at temperature T, pressure p & volume V as illustrated in Fig 1.

Assume the number of moles of individual gases be n₁, n₂,...etc. ,and their respective masses is m₁, m₂, ...etc. Later we have for overall number of moles n and net mass m

n = n₁+ n₂ + .....= ∑ n_i                       ...6.1

m = m₁ + m₂ +......=∑ m_i                ...6.2

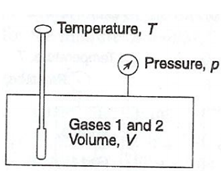
 Gas Mixture

Here i refer the number of each of  gas.

In the Dalton's model, each of the gas is conceived of as existing separately at the temperature T and net volume V of the mixture as illustrated in Figure 2.

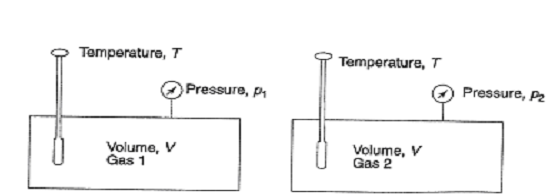
Illustrating Dalton's Model

If one were to compute the pressures exerted through individual gases, they would be found to be p₁,p₂, ....etc., like., less than the net pressure p of the mixture. These are referred as partial pressures. Letting mixture and each of component gas existing separately at T & V, we have for a binary gas mixture:

Therefore, for a mixture of ideal gases, the net pressure p is equivalent to the sum of the partial pressures. It is known as the Dalton's law of partial pressures.

                             p = p₁ + p₂ or p = ∑i p_i