Theorem II:

Consider A be the area of the plane curve APB in ZOX plane

Let a small elemental area dA at distance x from the z-axis, that is considered as the axis of rotation for the area A. Throughout the rotation θ around z-axis, elemental area dA moves through distance x θ.

Therefore, the solid volume δ V generated by this small area is given by

δV = dA × x θ

Total volume generated by the plane area A is, thus, given by

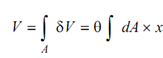
where, θ is the common angle of rotation for all of such type of elemental area dA.

∴ V = θ [ A x¯ ]

Here, x¯ is the x co-ordinate of the centroid of the area A

or                           V =  A × [ x¯ θ]

where, x¯ θ is the distance travelled by the centroid G of the area A during the rotation θ around the given axis z.