Extension of Parallel Axis Theorem:

Assume an unsymmetrical area A illustrated in Figure, where CX and CY are the centroidal axes and KX₁ and KY₁ are axes parallel to centroidal axes through a point K along with co-ordinate (x₁, y₁).

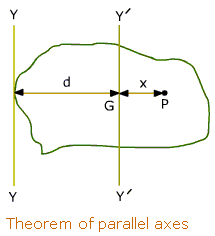
This can be proved that product of inertia I _{x1 ,y1}  with respect to axes KX₁ and KY₁ is always higher than I _x,y about axes CX and CY and is computed as given under :

I x₁  ,y ₁ = I _xy  +  A ( x₁ y₁ )

 This equation is similar to parallel axes theorem for moment of inertia of an area & you may note down that the product of inertia is hence minimum w.r.t. centroidal axes for given directions X and Y.