Method for Constructing X  and R Charts:

For a known value of standard deviation of the procedure distribution, the X  chart can be defined as

UCL_x¯¯ = X + z s_x and LCL _x¯¯ = X¯¯ - zs_x      

where,

s_x =s/√ n    = standard deviation of sample means,

s = standard deviation of the process distribution,

n = sample size,

X¯¯ = average of sample means or a target value set for the process, and

z = number of standard deviations for a specific confidence level (z = 3).

 An X chart is merely a plot of the means of the samples that were taken from a procedure, Whereas, R chart is a plot of the range in each sample. The range is the difference among the highest and the lowest numbers in that sample. Mathematically specking, it may be defined as :

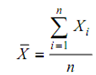
here,  X   is the mean of the sample, i is the item number and n is the total number of items in the sample.

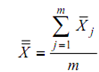
where, j is the sample number, m is the total number of samples, Rj is the difference between the highest and lowest measurements in the sample and R is the average of the measurement differences R for all of the samples, or

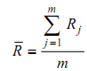
Therefore, upper and lower control limits may be defined as

Upper control limit for             X¯ = X¯¯ + A₂ R¯

Lower control limit for             X¯ = X¯¯ - A₂ R

Upper control limit for             R = D₄ R¯

Lower control limit for              R = D₃ R¯