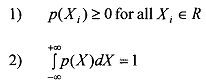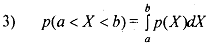Continuous Probability Distribution

A continuous random variable X has a zero probability of assuming exactly any of its values. Apparently, this seems to be a surprising statement. Let us, try to explain this by considering a random variable say, weight. Obviously weight is a continuous random variable since it can vary continuously. Suppose, we do not know the weight of a person exactly but have a rough
idea that her weight falls between 50 kg and 51 kg. Now, there are an infinite number of possible weights between these two limits. As a result, by its definition, the probability of the person assuming a particular weight say, 50.3 kg will be negligibly small; almost equal to zero. But we can definitely attach some probability to the person's weight being between 50 kg and 51 kg. Thus,
for a continuous random variable X, we assign a probability to an interval and not to a particular value. Here, we look for a function p(4, called the probability density function, such the with the help of this function we can - compute the probability

p(a < x < b), a and b are the limits of an interval (a, b) where. a < b.

A probability density function is defined in such a manner that the area under its curve bounded by x-axis is equal to one when computed over the domain of X for which p(Y) is defined. The probability density function for a continuous random variable X defined over the entire set of real numbers R should satisfy the following conditions.