Chi-Square Distribution

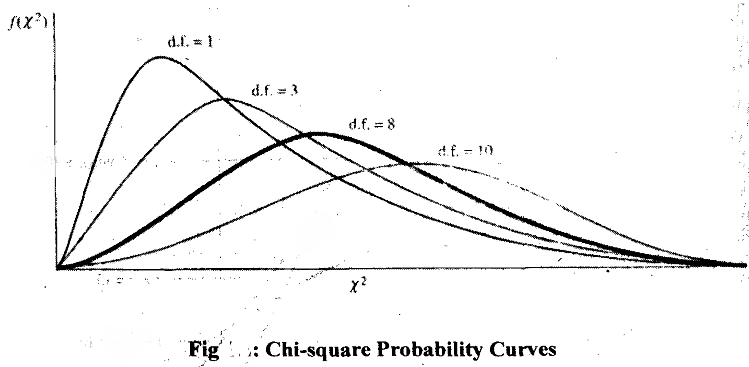
If z is a standard normal variate, as defined above, then the variable z² is said to be distributed as a variable with one degree of freedom. Since x² is a squared term, when z ranges from - oo to + oo, chi-squares ranges from 0 to + a,. Moreover, since z has a mean 0, most of the values taken by x² will be close to 0. As a result, probability density of x² distribution will be the maximum near 0. We can generalizc the above. If z₁, z₂ ,..... z_k are k independent chi-square variables then the variable

z = 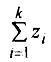, follows X² distribution with k degrees of freedom. We denote this by X_K²  , The probability density functions of for different degrees of freedom are given in Fig. Observe that as degree of freedom increases, the chi  distribution approaches normal distribution.