Lambert's Law:

Lambert (1760) and Bouguer independently studied the reduced in the intensity of radiation while it passes by a substance and made the following observations:

i) The amount of monochromatic light absorbed through a substance is proportional to the intensity of the incident light that is. the ratio of the intensity of the transmitted and incident light is constant.

ii) The intensity of the transmitted light decreases exponentially while the thickness of the substance, by that the light is passing, rises linearly.

These observations, known Lambert's law could be translated within a mathematical expression as describe below.

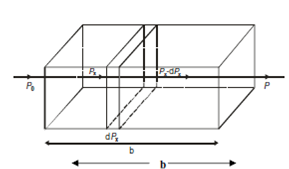
Figure: Illustration for establishing the Lambert's Law

In Figure, if P_o represents the radiant power of incident light and P represents the radiant power of transmitted light after passing by a slab of thickness b, consider a little slab of thickness d_x, then the change within power (dP_x), is proportional to the power of incident light (P_x) multiplied by the change in thickness (d_x) of the slab through which the light is passed. That is,

dP_x     ∝  P_xdx

or        dP_x =    k P_xdx

where k is the proportionality  constant  and the negative  sign implies  that  radiant power decreases with absorption. Eq. could be rearranged to Eq.

dP_x/P_x =  - kd_x

Integrating Eq. 2.2 inside the limits of P_o to P for intensity and 0 to b for the thickness we get,

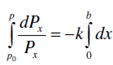
ln = P/P_O =-kb

 Eq. is a mathematical expression for Bouguer-Lambert law or Lambert's law. Changing this equation to base 10 logarithms and rearranging we get,

log P_o/P=      k/2.303          b = k 'b

Note that the ratio P/P_o has been inverted to remove the negative sign. Lambert's law applies to any homogeneous non-scattering medium, regardless of whether it is gas, liquid, solid, or solution.