Beer's Law:

In 1852, Beer and Bernard independently studied the dependence of intensity of transmitted light on the concentration of the solution. It was found that the relation between intensity of the transmitted light and concentration was exactly the same as found by Lambert for the intensity of the transmitted light and the thickness of the absorbing medium. Through mathematically, a Beer's observations can be expressed as follows.

Consider a monochromatic radiation beam of intensity P_x traversing any thickness of solution of a single absorbing substance of concentration c. If c is changed by a small amount  dc  to c  +  dc,  the  change  in transmitted  power  dP_x   is  proportional  to the incident intensity Px and dc. We could express it as follows.

dP_x  ∝ P_x  dc

dP_x = - k "P_x  dc

where k″ is the proportionality  constant  and the negative  sign implies  that radiant power decreases with absorption. This equation could be rearranged to:

dP_x/P_x = - k " dc

On integration inside the limits of P_o to P for intensity and 0 to c for concentration we get

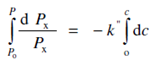
or ln = P/P_o =-k"c

or        log10 P_o/P = (k"/2.303)c

Eq. is a mathematical expression for Beer's law. The Lambert's and Beer's laws are combined and are expressed as per Eq.

log  P_o/P = abc

In this expression, 'a'  is a constant (combining two constants k′, k″ and the numerical factor)  and is known as  absorptivity  (earlier  called  extinction  coefficient)  whose  value depends  on  unit  of  concentration   used  and  is  a  function  of  wavelength  of  the monochromatic light used. A concentration is commonly expressed in terms of grams per dm³ and b in cm. Thus, it has units of c ^-1   g^-1 dm³.