Strain Energy due to Normal Stress:

Previously, you have learnt a few of the features of elastic solids. Here, we shall learn one more important features. Whenever forces are applied on elastic (deformable) solids, the points of application of the forces move because of deformations in the solid, and thus they do work, loosing their potential energy within the process. In elastic solids this energy is fully stored and released while the strains are removed. This stored energy is known as Strain Energy.

Now let us develop an expression for the strain energy stored in the solid, although it is subjected to a general stress, say σ_x.

Assume a little element of dimensions dx, dy and dz as shown in Figure, and subjected to a normal stress σ_x that generates an elongation dδ in the direction of the stress.

If E is the Young's Modulus of the material,

strain produced, ε_x =σ_x/E

∴          elongation dδ = dx .ε_x =dx. σ_x/E

Total force applied on the element dF, is given through the stress multiplied through area on that it is applied.

dF = σ_x .dy.dz

Work done through dF = Force × Average Displacement

dU =dF.dδ/2

dU = ½ σ_x.dy.dz .σ_x/E dx

dU = 1/2E σ²_x.dx.dy.dz

As dx . dy . dz represents the volume of the element dv.

dU = (σ²_x/2E) dv                                                                                                          . . . (15)

(By same reasoning, because of other normal stress components the energy stored in the element may be shown to be(σ²_x/2E) dv and(σ²_z/2E) dv.

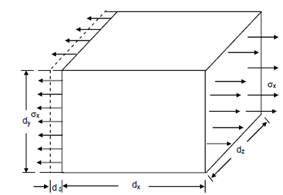
Figure

Total energy stored in the solid,

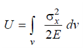
Dividing Eq. (3.15) by dv, we can also obtain an expression for the strain energy density at any point as

u = σ²_x/2E

 (Also the strain energy density due to other stress components may be shown to be σ²_y/2E and   σ²_z/2E respectively).

The application of Equations (15), (16) and (17) will be dealt elaborately in a later unit. However, these expressions are presented here, as they are useful in the study of a given state of stress and will be explained further.