Strain Energy Due To Normal Stress:

You have learnt a few of the characteristics of elastic solids in previous unit. Here, we will learn one more significant characteristic. Whenever forces are applied on elastic (deformable) solids, the points of application of the forces move because of deformations in the solid, and therefore they do work, loosing their potential energy in the procedure. In elastic solids this energy is completely stored & released while the strains are eliminated. This stored energy is called as Strain Energy.

Now let us make an expression for the strain energy stored in the solid, while it is subjected to a normal stress, say s_x.

Let a small element of dimensions dx, dy and dz as illustrated in Figure and subjected to a normal stress s_x which generated an elongation dd in the direction of the stress.

If E is the Young's Modulus of the material,

            strain generated, e x  =    s_x / E

∴ elongation d d = dx . e _x  = dx .   s _x/ E

Entire force applied on the element dF, is specified by the stress multiplied by area on that it is applied.

i.e.

dF = s _x  . dy . dz

∴          Work done by dF = Force x Average Displacement

i.e.

 dU = dF . (d d / 2)

dU = 1 /2 s_x . dy . dz . (s_x/ E)  dx

dU = ( 1 / 2E )s² x. dx . dy . dz

Since dx . dy . dz represents the volume of the element dv.

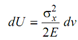
 (By same reasoning, because of other normal stress components the energy stored in the element might be shown to be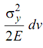and .)

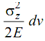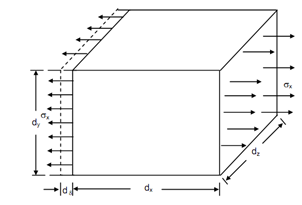
    Figure

Total energy stored in the solid,

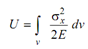
Dividing Eq. (15) by dv, we can also obtain an expression for the strain energy density at any point as

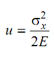
 (Also the strain energy density due to other stress components may be shown to be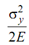  and 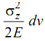 respectively).