Circular Representation of State of Stress:

From a state of stress defined by the components σ_x, σ_y and τ_xy, we express the stress components on an arbitrary plane as

σ = (σ_x+σ_y/2) + (σ_x - σ_y/2) cos 2θ +τ_xy sin 2θ

τ = -(σ_x - σ_y/2) sin 2θ +τ_xy cos 2θ

which we may rewrite in general as

(i) σ = a+b cos 2θ +c sin 2θ

(ii) τ = -b sin 2θ +c cos 2θ

Let us now try to establish direct relationship between σ and τ by eliminating θ between Eqs. (i) and (ii).

To simplify the effort, let us take the origin of coordinate at (a, 0), so that the new variable σ¯ = (σ - a) is considered for developing the relationship.

(iii) σ¯ = b cos 2θ + c sin 2θ

τ = - b sin2θ + c cos 2θ                                   . . . (iv)

Squaring and adding, we get

 σ¯² + τ² = b² cos² 2θ +c² sin² 2θ + 2bc cos 2θ. Sin 2θ

+ b² sin² 2θ +c² cos² 2θ -2bc cos 2θ sin 2θ

= b² (cos² 2θ+ sin² 2θ) +c² (sin² 2θ + cos² 2θ)

i.e. σ¯²  +τ² = b² + c²

Since b and c are constants let b²  + c²  = r ²

∴ σ¯²  +τ² = r ²

Eq. (14) shows that if σ and τ, the normal and shear stress components on any arbitrary plane are plotted as coordinates, a locus of the point will be a circle whose centre will be ((σx +σy/2), 0) and radius will be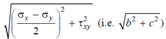.