Maximum Shear Stress:

We have the general expression for shear stress as

tnt = txy cos 2q - ((sx - sy)/2) sin 2q                    ...(1)

With respect to q, & equating the derivative to zero,

dt_nt / dq  = -2 t_xy sin 2q - (σ_x - σ_y) cos 2q= 0

∴          tan 2q = - (s_x - s _y ) / 2t_xy                         .........(2)

 Since the planes on which maximum shear stresses occur are specific set of planes we may denote them distinctly by Y (instead of general aspect angle q). Comparing Eqs. (1) and (2), we conclude that 2Y = 2f ± 90º as tan 2f. tan 2Y = - 1.

∴          Y = f ± 45º   ................ (3)

 Eq. (3) mentions that the planes of maximum shear stress bisect the right angles between the major & minor principal planes.

The normals to the major & minor principal planes might now be described as the major and minor principal axes. If the principal stresses & principal planes are known, further analysis might be simplified by expressing the state of stress w.r.t. a new coordinate system along major & minor principal axes as coordinate axes themselves. Usually these axes are called axes 1 and 2 respectively.

The common expressions for stress components on arbitrary planes whose aspect angle  might now be measured with axis-1 as reference axis.

Hence,

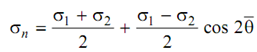           ------------ (4)

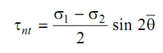                       ------------- (5)

Eq. (3) already defines that  should be ± 45º for t_nt to be maximum.

Thus,

 t _{max, min}  =  s ₁ -s₂  sin (± 90^o )

∴          t_max =  (s₁ - s₂)/2

and

                t_min =   - (s₁ - s₂)/2                             ----------(6)

As the sign of maximum shear stress is not significant, expression for t_min is not generally utilized. Let us have a few instance.