Expressions of Principal Stresses:

Further, the second derivatives, d²σ_n/dθ , will be negative for the solution σ₁ (aspect angle of the major principal plane) and positive for the solution σ₂ (aspect angle of the minor principal plane). Let us obtain these expressions too.

d²σ_n/dθ   = d/dθ (dσn/dθ) = 2(σy-σx/2)2 cos 2θ -2τ_xy sin2θ)

d²σ_n/dθ   = 4(σy-σx/2)2 cos 2θ -2τ_xy sin2θ)

After obtaining the solutions σ1 and σ2 of Eq. (2), their values may be substituted in the d²σ_n/dθ expression for given in Eq. (3) and the major and minor principal planes may be identified. But in practical solutions this step is rarely required. Instead, substitute the two solutions σ1 and σ2 in the expression for normal stress and obtain the values of principal stresses σ1 and σ2 and corresponding principal planes may be identified.

Now, let us derive the general expressions for the principal stresses. Since, we know that tan 2Φ = 2τ _xy/σ _x - σ _y  on a principal plane, we may write as

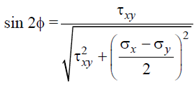
And

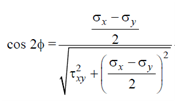
Substituting Eqs. (4) and (5) in the expression for σn, we obtain

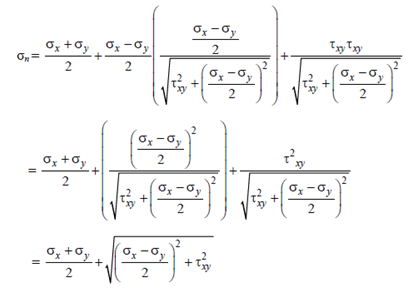
Since 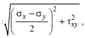will have two roots namely ±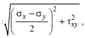, we may write the final expression for major and minor principal stresses as follows :

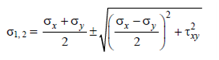
Eqs. (2) and (6) may be used to readily determine the principal planes and principal stresses.

Now let us have an example for determination of principal stress and principal planes, given the state of stress.